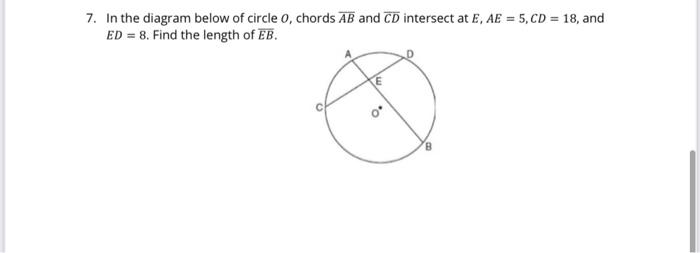
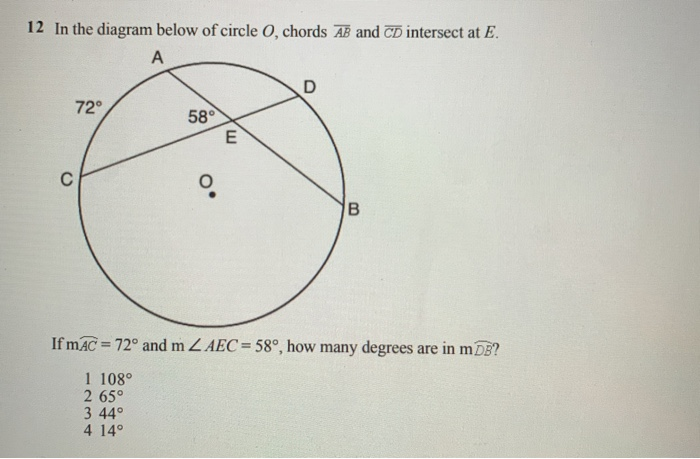
39 in the diagram below of circle o chords ab and cd intersect at e

In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: (i) ΔAPC and ΔBPD are similar. (ii) If BD = 2.4 cm AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC. Answer 1. Two line segments AB and CD intersect each other at P. Example 3 In figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠ AEB = 60°. Given: AB is diameter of circle Chord CD, where CD = Radius of circle To prove: ∠AEB = 60° Construction: Join OC

Prove that, if two lines containing chords of a circle intersect each other outside the circle, then the measure of angle between them is half the difference in measures of the arcs intercepted by the angle. (Textbook pg. no. 72) Given: Chord AB and chord CD intersect at E in the exterior of the circle.

In the diagram below of circle o chords ab and cd intersect at e

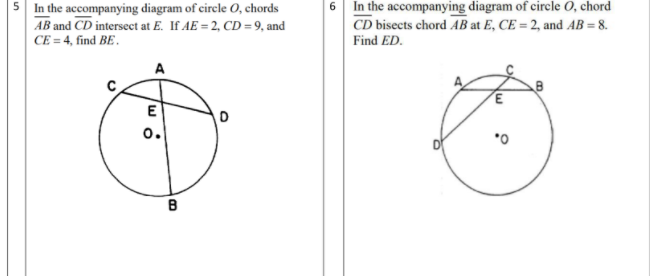
In the accompanying diagram of circle o, chords ab and cd intersect at e. if ae x eb = 18 and ed = 6, what is … Get the answers you need, now! frix77 frix77 05/05/2021 Mathematics High School answered In the accompanying diagram of circle o, chords ab and cd intersect at e. if ae x eb = 18 and ed = 6, what is ce? a: 108 b: 24 c: 3 d: 18 1 See ... Example 1(Method 1) Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact. Given: Let two concentric circles be C1 & C2 with center O AB be chord of the larger circle C1 which touches the smaller circle C2 a Cd formula trigonometry. By subtracting the x-coordinates of C and E we find the length of the line. If the two endpoints of the chord CD meet at point P then CPD is known as the angle extends by the chord CD at point P. Chord Length Formula Using Trigonometry. Sinc2 In the above formula for the. R 2 d 2 Chord Length Using Trigonometry.

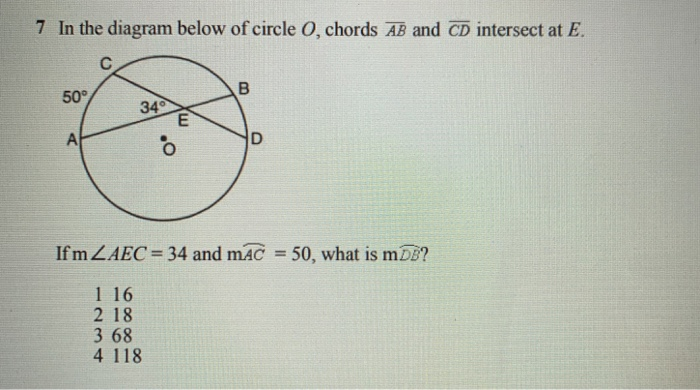
In the diagram below of circle o chords ab and cd intersect at e. Find an answer to your question In the diagram below of circle 0, diameter AB is parallel to chord CD. A. 110° B. 70° C. 55° D. 35° If mCD= 70, what is mAC? Knownasniya Knownasniya 02/02/2021 Mathematics High School answered In the diagram below of circle 0, diameter AB is parallel to chord CD. The angle between the tangent to a circle and the chord drawn from the point of contact is equal to the angle ... (1) 9.2 In the diagram below, two unequal circles intersect at A and B. AB is produced to C such that CD is a tangent to the circle ABD at D. F and G are points on the smaller circle such that CGF and DBF are straight lines. O is the centre of the circle and AB is a chord. AC is the bisector of ∠OAB. ∠OAB = 56°. a. Prove that OC and AB are parallel, b. Find ∠ABC and ∠OBE. Answer: Question 27. O is the centre of the circle. AD and BC are perpendicular to XY. CB cuts the circle at E. Prove that -CE = AD. Answer: ∠AEB = 90° (Angle in a semi circle) ( 1 ... In the diagram below, RS, ST and TR are tangent to circle O at A, B, and C respectively. ... Suppose a circle has two chords, AB and CD, that intersect at a point E, such that AE = 10, AB = 14 ...

Now, suppose RS = x. The diagram for the same is shown below. Consider the ΔPOR, OP 2 = OR 2 +PR 2 ⇒ 5 2 = (4-x) 2 +PR 2 ⇒ 25 ... the chord AB is equal to the radius of the circle. In the above diagram, OA and OB are the two radii of the circle. Now, consider the ΔOAB. ... Here chords AB and CD intersect each other at O. Consider ΔAOB ... Answer: Use a diagram similar to that in Exercise 1. Given: Circle C with diameter , chord , and ⊥. Prove: bisects. ⊥ Given. ∠AFC and ∠BFC are right angles Definition of perpendicular lines. AFC and BFC are right triangles Definition of right triangle. ∠AFC ≅∠BFC All right angles are congruent. Two chords AB and AC of a circle C(O, r), such that AB and AC are equally inclined to diameter AOD. Example 6: Two equal chords AB and CD of a circle with centre O, when produced meet at a point E. Prove that BE = DE and AE = CE. Solution: Given. Two equal chords AB and CD intersecting at a point E. To prove. BE = DE and AE = CE. In the adjoining figure, CD is a diameter of the circle with centre O. Diameter CD is perpendicular to chord AB at point E. Show that ∆ABC is an isosceles triangle. Given: O is the centre of the circle. diameter CD ⊥ chord AB, A-E-B To prove: ∆ABC is an isosceles triangle. Proof: diameter CD ⊥ chord AB [Given]

7.2 In the given diagram, O is the centre of the circle. Points A, C, B and E are on the circle. Diameter COE and chord AB intersect at right angles at D. AD = DB = 15 cm and CD = 6 cm. 7.2.1 Calculate the length of DO. (4) 7.2.2 Calculate the size of AOB. (3) 7.3 The figure below models the wheel of a sport car with O the central point through ... In the diagram below, O is the centre of the circle of radius 8cm. BA and BC are tangents to the circle at A and C respectively. PD is the diameter and AC is a chord of length 8cm. Angle ADC = 120 o. ARC is an arc of the circle, Centre B and radius 4.6cm. Properties of Circle: We see many circular shapes in our daily life like coins, bicycle wheels, etc. All points on the circle's boundary are equidistant from a fixed point called the centre. The radius of a circle is a line segment connecting the centre of the circle to any point on the circle's boundary. In circle O, perpendicular chords AB and CD intersect at E so that AE= 2, EB= 12 and CE= 4. Find the radius of circle O and the shortest distance from E to the circle. What are circle theorems?

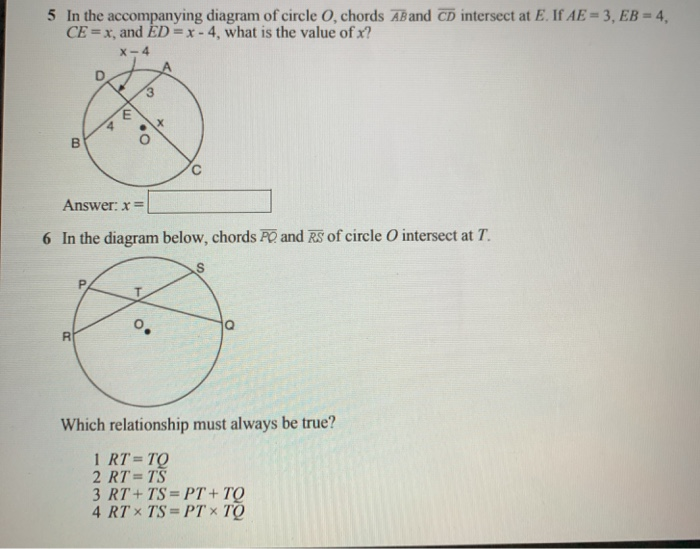
The distance between chords $\overline{PQ}$ and $\overline{RS}$ is 4, and the distance between chords $\overline{RS}$ and $\overline{TU}$ is . trig. In a diagram of circle, chords AB and CD intersect at E. If AE = 3, EB = 4, CE = x, and ED = x - 4, what is the value of x? Geometry. Given: ∆ABC, m∠A = 35°, Circle k(O, r=3), O∈ AB, AB is a ...

Q2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite of its center If the distance parallel between AB and CD is 6 cm Find the radius of the circle. Solution:- AB = 5 cm. CD = 11 cm. MB = 2.5 cm. ND = 5.5 cm . Let OM = x cm and ON = 6 - x cm. ∆OMB. By Pythagoras theorem ...

An annulus is a ring bounded by two concentric circles. In annulus A has an inner circle of radius 2 cm and an outer circle of radius 6 cm. Annulus B has an outer circle of radius 9 cm. If annulus B has an area equal to that of . trig. In a diagram of circle, chords AB and CD intersect at E.

The figure given below, shows a circle with centre O. Given: ∠ AOC = a and ∠ ABC = b. (i) Find the relationship between a and b (ii) Find the measure of angle OAB, if OABC is a parallelogram. Solution: Question 24. Two chords AB and CD intersect at P inside the circle.

In the given diagram ';O is the centre of the circle and AB is parallel to CD. AB = 24 cm and distance between he chord AB and CD is 17 cm. It the radius of the circle is 13 cm, find the length of the chord CD.

Two chords AB and CD of lengths 5 cm and 11 cm, respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle. Solution: Let O be the centre of the given circle and let its radius be cm.

The diagram shows four straight lines, $\D AD, BC, AC$ and $\D BD.$ Lines $\D AC$ and $\D BD$ intersect at $\D O$ such that angle $\D AOB$ is $\D \frac{\pi}{6}$ radians. $\D AB$ is an arc of the circle, centre $\D O$ and radius 10 cm, and $\D CD$ is an arc of the circle, centre $\D O$ and radius 20 cm.

In the diagram below of circle O, diameter AB is perpendicular to chord CD at E. If AO = 10 and BE = 4, find the length of CE. Answer: Since diameter AB is perpendicular to CD, it also bisects CD. If you draw OC and OD, they will both be radii equal to AO, which is 10. You will also have two right triangles. OC = 10. OE = OB - BE = 10 - 4 = 6.

Two chords AB and CD of a circle intersect each other at P outside the circle. If AB = 5 cm, BP = 3 cm and PD = 2 cm, find CD. ... If AB is a chord of length 6 cm of a circle of radius 5cm, the tangents at A and B intersect at a point X (figure), then match the columns. ... BC = 10 cm and CA = 12 cm as shown in figure. Observe the diagram and ...

(a) In the figure (i) given below, AB is a diameter of a circle with centre O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED. (b) In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED. Answer 13

Cd formula trigonometry. By subtracting the x-coordinates of C and E we find the length of the line. If the two endpoints of the chord CD meet at point P then CPD is known as the angle extends by the chord CD at point P. Chord Length Formula Using Trigonometry. Sinc2 In the above formula for the. R 2 d 2 Chord Length Using Trigonometry.

Example 1(Method 1) Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact. Given: Let two concentric circles be C1 & C2 with center O AB be chord of the larger circle C1 which touches the smaller circle C2 a